This is mostly a note to myself.
Way back in the dawn of the modern-macro era, the fresh-water Chicago kids came up with Real Business Cycle theory where they endogenised the labour supply and claimed that macro variation was explained by productivity shocks.
The salt-water gang then accepted the techniques of RBC but proposed a bunch of demand-side shocks instead.
The big criticism of productivity shocks has always been to ask how you can realistically get negative shocks to productivity. Technological regress just doesn’t seem all that likely.
Now, models of credit cycles like Kiotaki (1998) show how a small and temporary negative shock to productivity can turn into a large and persistent downturn in the economy. In short: Credit constraints mean that some wealth remains in the hands of the unproductive instead of being lent to the productive sectors of the economy. The share of wealth owned by the productive is therefore a factor in aggregate output. A temporary negative shock to productivity keeps more of the wealth with the unproductive for production purposes and it takes time for the productive sector to accumulate its wealth back. If some sort of physical capital (e.g. land) is used as collateral, the shock will also lower the price of the capital, thus decreasing the value of the collateral and so imposing tighter restrictions on credit.
But Kiyotaki’s model still requires some productive regress …
Looking at Aiyagari (1994) and Castaneda, Diaz-Gimenez and Rios-Rull (2003) today (lecture 3 by Michaelides in EC442), I realise that small negative productivity shocks are conceptually okay if they’re applied idiosyncratically (i.e. individually) to labour.
Let  be your efficiency state in period
be your efficiency state in period 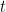 .
.  is a Markov process with transition matrix
is a Markov process with transition matrix 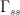 .
.  is the efficiency of somebody in state
is the efficiency of somebody in state  . Castaneda, Diaz-Gimenez and Rios-Rull use this calibration, taken from the data:
. Castaneda, Diaz-Gimenez and Rios-Rull use this calibration, taken from the data:
| State |
s=1 |
s=2 |
s=3 |
s=4 |
| e(s) |
1.00 |
3.15 |
9.78 |
1,061.00 |
| Share of population |
61.1% |
22.35% |
16.50% |
0.05% |
The transition matrix would be such that the population-shares for each state are stationary.
A household’s labour income is then given by 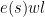 .
.
A movement from s=3 to s=2, say, is therefore a negative labour productivity shock for the household.
The trick is to think of the efficiency states as job positions. Somebody moving from s=3 to s=1 is losing their job as an engineer and getting a job as an office cleaner. They will probably increase  to partially compensate for the lose in hourly wage (
to partially compensate for the lose in hourly wage (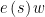 ).
).
Remember that in the (Neo/New) Classical models, there’s an assumption of zero unemployment. However much you want to work, that’s how much you work. [That might sound silly to a casual reader, but it’s okay as a first approximation. There are (i.e. search-and-matching) models out there that look at unemployment and can be fitted into this framework.]
If everybody is equally good at every job position (as we have here) and all the idiosyncratic shocks balance out so the population shares are constant, then – I believe – there shouldn’t be any change in observed aggregate productivity.
However, if you introduced imperfect transfer of ability across positions so that efficiency becomes  where
where  is your private type per job position, then idiosyncratic shocks could therefore show up in aggregate numbers.
is your private type per job position, then idiosyncratic shocks could therefore show up in aggregate numbers.
This is essentially an idea of mismatching. A senior engineering job is destroyed and a draftsman job is created both in Detroit, while the opposite occurs in Washington state. Since the engineer in Detroit can’t easily move to Washington, he takes the lower-productivity job and a sub-optimal person gets promoted in Washington.